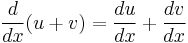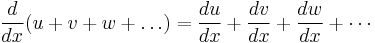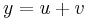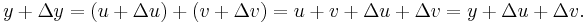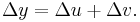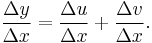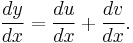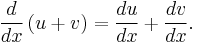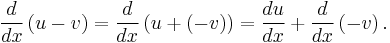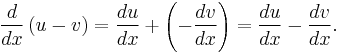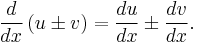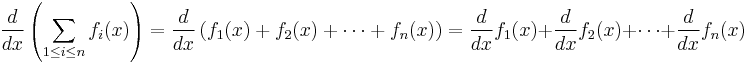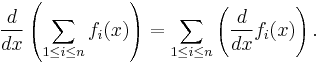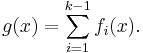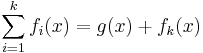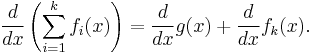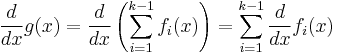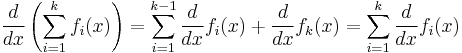Sum rule in differentiation

In calculus, the sum rule in differentiation is a method of finding the derivative of a function that is the sum of two other functions for which derivatives exist. This is a part of the linearity of differentiation. The sum rule in integration follows from it. The rule itself is a direct consequence of differentiation from first principles.

The sum rule tells us that for two functions u and v:

\frac{d}{dx}(u %2B v)=\frac{du}{dx}%2B\frac{dv}{dx}

This rule also applies to subtraction and to additions and subtractions of more than two functions

\frac{d}{dx}(u %2B v %2B w %2B \dots)=\frac{du}{dx}%2B\frac{dv}{dx}%2B\frac{dw}{dx}%2B\cdots

Proof

Let y be a function given by the sum of two functions u and v, such that:

y = u %2B v \,

Now let y, u and v be increased by small increases Δy, Δu and Δv respectively. Hence:

y %2B \Delta{y} = (u %2B \Delta{u}) %2B (v %2B \Delta{v}) = u %2B v %2B \Delta{u} %2B \Delta{v} = y %2B \Delta{u} %2B \Delta{v}. \,

So:

\Delta{y} = \Delta{u} %2B \Delta{v}. \,

Now divide throughout by Δx:

\frac{\Delta{y}}{\Delta{x}} = \frac{\Delta{u}}{\Delta{x}} %2B \frac{\Delta{v}}{\Delta{x}}.

Let Δx tend to 0:

\frac{dy}{dx} = \frac{du}{dx} %2B \frac{dv}{dx}.

Now recall that y = u + v, giving the sum rule in differentiation:

\frac{d}{dx}\left(u %2B v\right) = \frac{du}{dx} %2B \frac{dv}{dx} .

The rule can be extended to subtraction, as follows:

\frac{d}{dx}\left(u - v\right) = \frac{d}{dx}\left(u %2B (-v)\right) = \frac{du}{dx} %2B \frac{d}{dx}\left(-v\right).

Now use the special case of the constant factor rule in differentiation with k=−1 to obtain:

\frac{d}{dx}\left(u - v\right) = \frac{du}{dx} %2B \left(-\frac{dv}{dx}\right) = \frac{du}{dx} - \frac{dv}{dx}.

Therefore, the sum rule can be extended so it "accepts" addition and subtraction as follows:

\frac{d}{dx}\left(u \pm v\right) = \frac{du}{dx} \pm \frac{dv}{dx}.

The sum rule in differentiation can be used as part of the derivation for both the sum rule in integration and linearity of differentiation.

Generalization to sums

Consider a set of functions f1, f2,..., fn. Then

\frac{d}{dx} \left(\sum_{1 \le i \le n} f_i(x)\right) = \frac{d}{dx}\left(f_1(x) %2B f_2(x) %2B \cdots %2B f_n(x)\right) = \frac{d}{dx}f_1(x) %2B \frac{d}{dx}f_2(x) %2B \cdots %2B \frac{d}{dx}f_n(x)

so

\frac{d}{dx} \left(\sum_{1 \le i \le n} f_i(x)\right) = \sum_{1 \le i \le n} \left(\frac{d}{dx}f_i(x)\right) .

In other words, the derivative of any sum of functions is the sum of the derivatives of those functions.

This follows easily by induction; we have just proven this to be true for n = 2. Assume it is true for all n < k, then define

g(x)=\sum_{i=1}^{k-1} f_i(x).

Then

\sum_{i=1}^k f_i(x)=g(x)%2Bf_k(x)

and it follows from the proof above that

\frac{d}{dx} \left(\sum_{i=1}^k f_i(x)\right) = \frac{d}{dx}g(x)%2B\frac{d}{dx}f_k(x).

By the inductive hypothesis,

\frac{d}{dx}g(x)=\frac{d}{dx} \left(\sum_{i=1}^{k-1} f_i(x)\right)=\sum_{i=1}^{k-1} \frac{d}{dx}f_i(x)

so

\frac{d}{dx} \left(\sum_{i=1}^k f_i(x) \right) = \sum_{i=1}^{k-1} \frac{d}{dx}f_i(x) %2B \frac{d}{dx}f_k(x)=\sum_{i=1}^k \frac{d}{dx}f_i(x)

which ends the proof of the sum rule of differentiation.

References